Una ecuación algebraica de segundo grado1 2 o simplemente ecuación cuadrática de una variable es una ecuación algebraica que conlleva una expresión algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un trinomio de segundo grado o binomio de segundo grado. La expresión general de una ecuación cuadrática de una variable es:
donde x representa la variable, y donde a, b y c son números enteros 3 ; a es el coeficiente cuadrático o principal (distinto de 0), b el coeficiente lineal o coeficiente del término de primer grado, y c es el término independiente 4 .
Este polinomio, si los coeficientes son números racionales (excepcionalmente, números reales), se puede representar mediante la gráfica de una función cuadrática, es decir, por una parábola. Esta representación gráfica es útil, porque las intersecciones o punto tangencial de esta gráfica, en el caso de existir, con el eje X coinciden con las soluciones reales de la ecuación.
A la variable x, algunos llaman indeterminada 5 otros llaman incógnita
Definición en el dominio de los reales
Una ecuación algebraica se puede plantear en diferentes conjuntos numéricos. Justamente alguien dice con polinomios con coeficientes en ℂ 7 . Sin embargo se presenta en el caso que se trabaje en ℝ.
Una ecuación cuadrática se puede escribir en la forma
son números reales y 
. En la actualidad la herramienta principal para la resolución de tales ecuaciones es la factorizazión . Si la ecuación se reduce a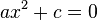 
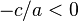las raíces son imaginarias 
No hay comentarios:
Publicar un comentario